王林军教授课题组提出细致互补自洽方法:波函数决定粒子如何跳跃,粒子决定波函数如何坍缩
近日,我系王林军教授课题组以“Detailed Complementary Consistency: Wave Function Tells Particle How to Hop, Particle Tells Wave Function How to Collapse”为题在物理化学核心期刊The Journal of Physical Chemistry Letters上发表研究论文(J. Phys. Chem. Lett. 2024, 15, 6771-6781)。该工作揭示了细致内在自洽性对混合量子-经典动力学的本征重要性,提出了细致互补自洽方法,即:波函数决定粒子如何跳跃,粒子决定波函数如何坍缩,回答了物理学和理论化学中长期存在的同时采用量子力学与经典力学时如何正确处理量子-经典关联的问题。该论文的第一署名单位为浙江大学化学系,作者包括:浙江大学博士生璜磊和施哲存,通讯作者为浙江大学王林军教授。本研究得到了国家自然科学基金(22273082)的资助。
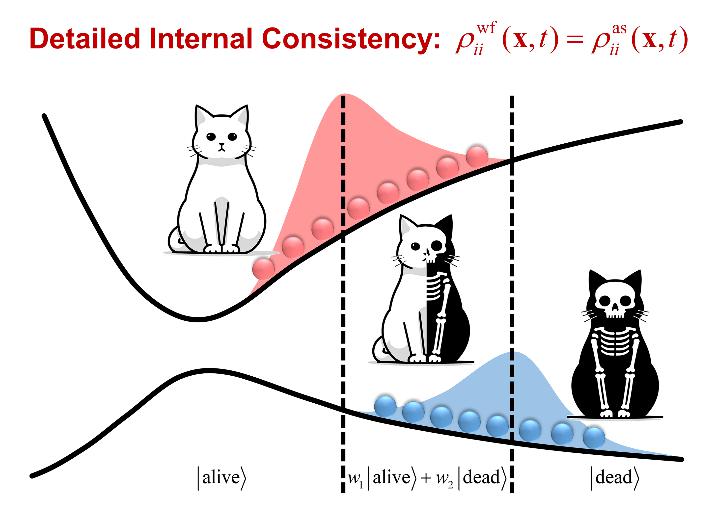
在化学、物理、生物和材料等多学科中,许多重要的过程(如质子转移、电荷传输、激子扩散、能量弛豫和单线态裂分等)都属于非绝热动力学的范畴。这些过程中存在量子跃迁,导致传统的玻恩-奥本海默近似不再适用,电子与核运动强烈耦合,是理论化学研究的重要科学问题之一。混合量子-经典动力学将体系中部分自由度进行经典力学处理,原则上可以达到更好的精度和效率平衡,有望应用于复杂大体系的非绝热动力学模拟,但是还需要发展更完善的理论方法。
在化学中广泛使用的轨线面跳跃混合量子-经典动力学方法中,同时存在波函数描述和占据数描述。虽然这两种描述都用于刻画同一概率分布,但是通常会给出不同的结果,一般占据数的结果更为可靠。该工作提出了混合量子-经典动力学应该满足细致内在自洽性,即:在任意时刻空间上的任意位置,波函数统计的布居分布都与占据数分布严格相等。我们进而提出了细致互补自洽(Detailed Complementary Consistency, DCC)方法,通过保证每条轨线的局域轨线占据数与其波函数计算的布居一致,实现了整个轨线系综始终保持细致内在自洽性。我们系统测试了采用占据数和波函数进行轨线分析的最少面跳跃(FSSH-as和FSSH-wf)方法,以及采用占据数和波函数进行轨线分析的细致互补自洽(DCC-as和DCC-wf)方法。除了标准的三个一维Tully散射模型,在更复杂的二维散射模型(图1所示Subotnick等提出的STD-1和STD-2模型)、一维二能级谐振子模型(图2所示Agostini等提出的BS-1、BS-2和BS-3模型)、一维三能级光解离模型和三维吡嗪模型(见图3,分别由Miller等和Domcke等提出)中,DCC方法都得到了与全量子精确解非常接近的结果,精度比目前领域内广泛采用的FSSH方法有系统性的大幅提升。特别地,FSSH方法结果严重依赖于其轨线分析算法,而DCC方法在两种轨线分析算法下给出了完全一致的高精度结果。
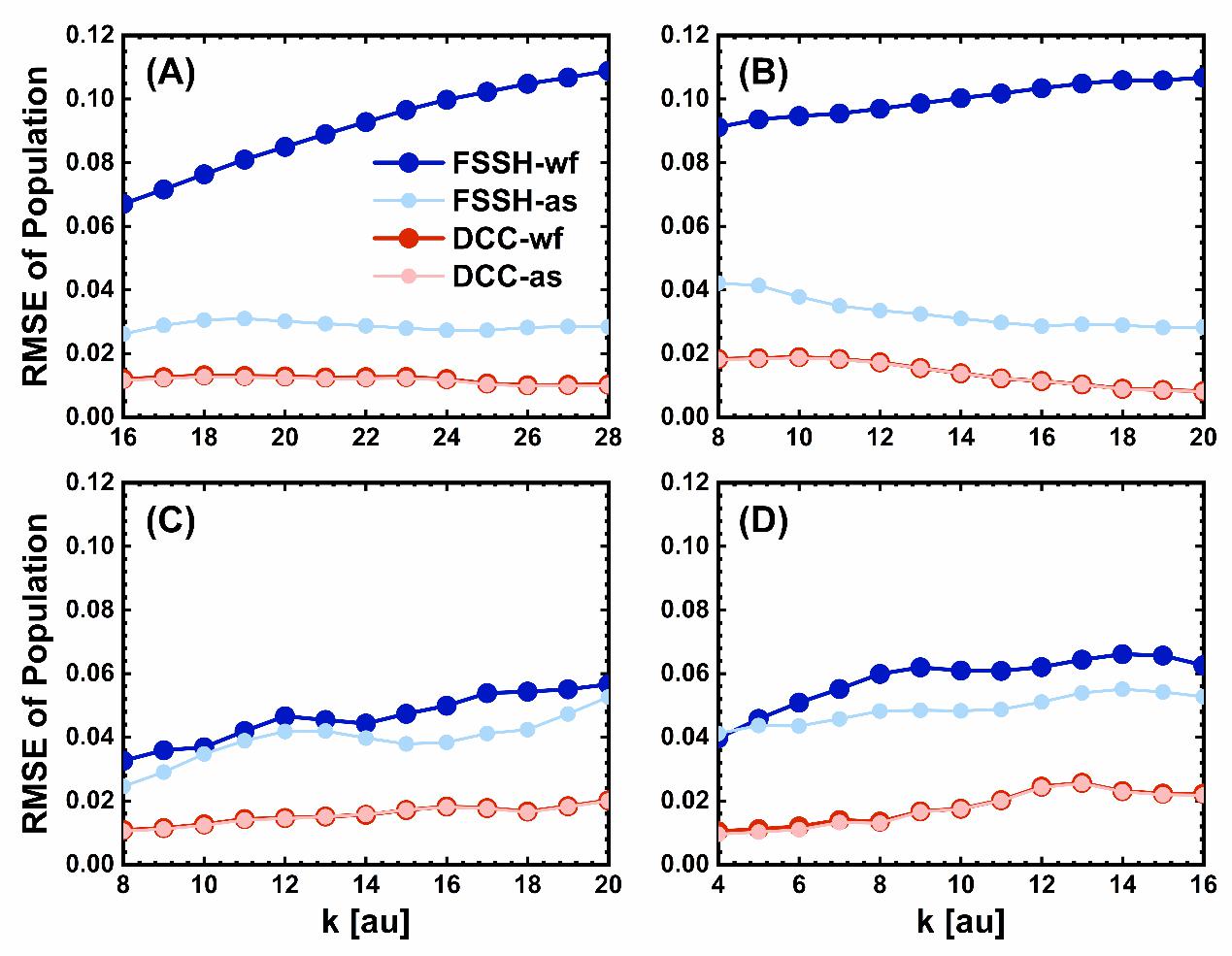
图1初始从(A)基态和(B)激发态出发,STD-1模型在不同初始位置和入射角下的布居均方误差与初始动量之间的关系。初始从(A)基态和(B)激发态出发,STD-2模型在不同初始位置和入射角下的布居均方误差与初始动量之间的关系。FSSH-wf、FSSH-as、DCC-wf和DCC-as的结果分别由蓝色、浅蓝色、红色和浅红色实心圆表示。
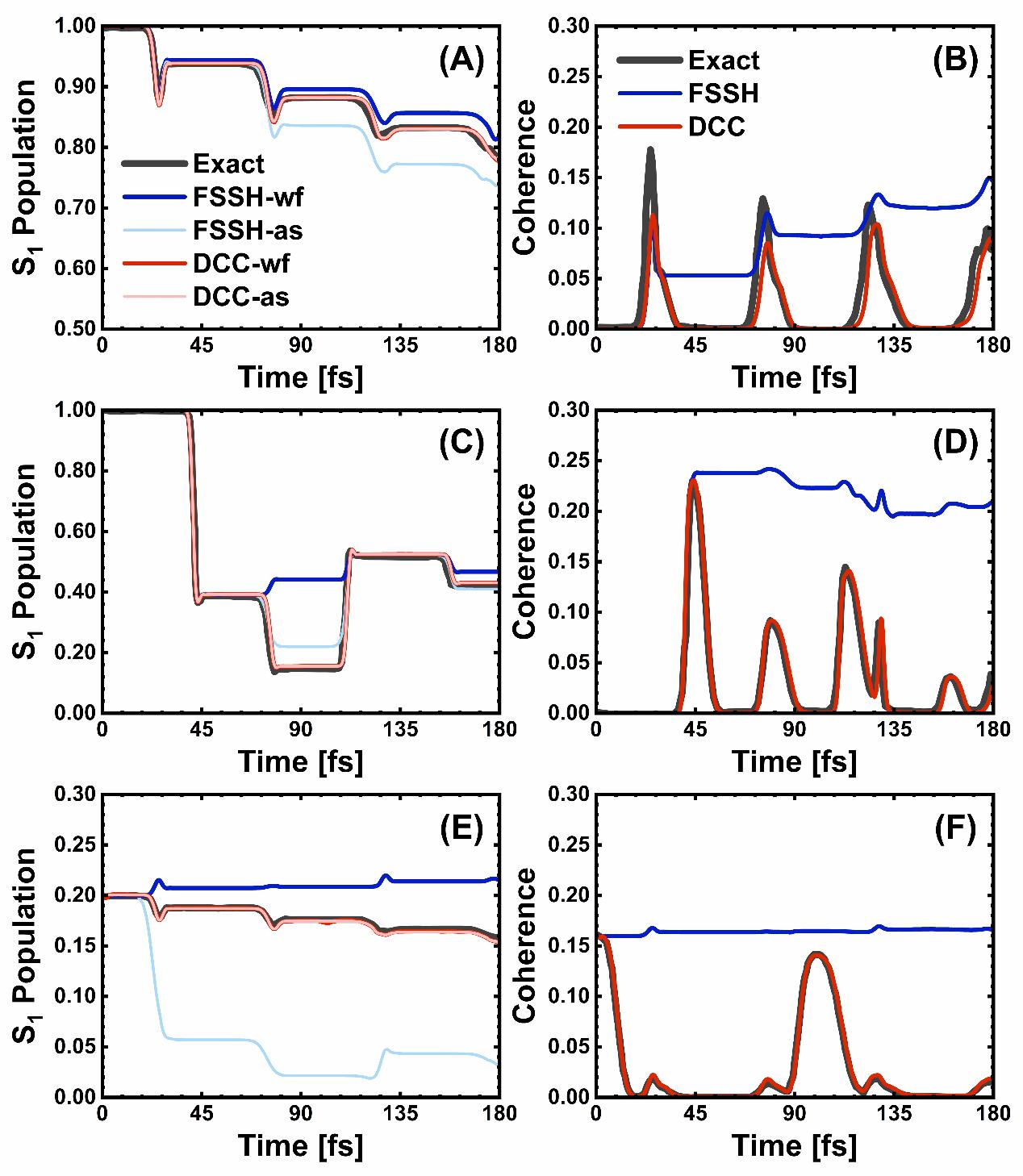
图2 (A, B)BS-1模型、(C, D)BS-2模型和(E, F)BS-3模型的激发态布居和相干随时间的变化。黑线表示精确的全量子动力学结果。在(A, C, E)图中,FSSH-wf、FSSH-as、DCC-wf和DCC-as的结果分别由蓝色、浅蓝色、红色和浅红色线表示。在(B, D, F)图中,FSSH和DCC的结果分别由蓝色和红色线表示。
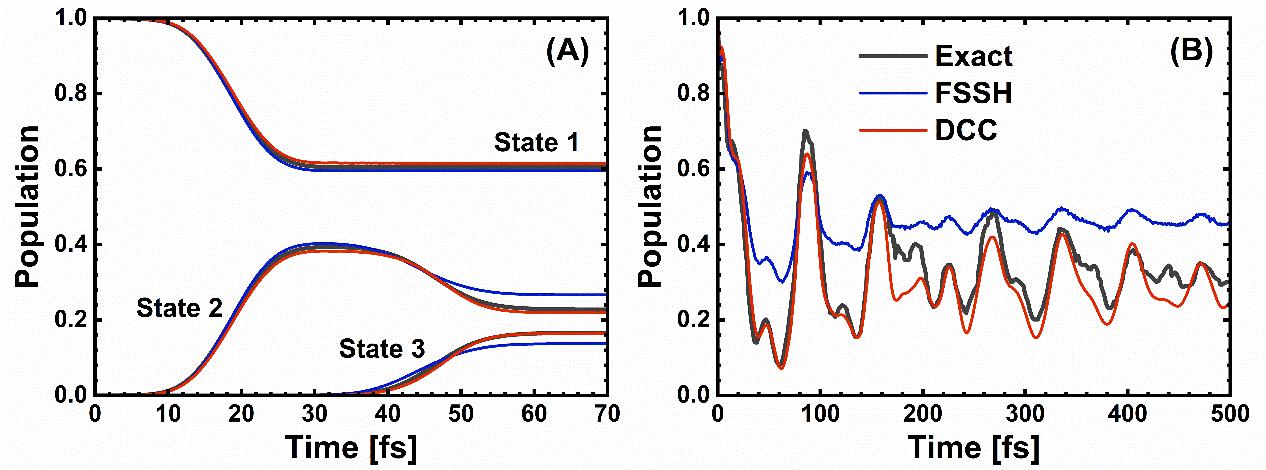
图3 (A)一种光解模型中所有透热态的布居随时间的变化,(B)三维吡嗪模型中透热2态布居随时间的变化。黑线表示精确的全量子动力学结果,FSSH和DCC分别由蓝线和红线表示。
我们提出的DCC方法能够始终保持细致内在自洽性,将势能面间跳跃与波函数坍缩这两种领域内原本分别研究的概念自然地统一在一起,作为细致内在自洽性的两面。在所有测试的具有局域非绝热耦合的散射和束缚态模型中,无论使用占据数还是波函数进行轨线分析,DCC方法都展现了很高的精度。从某种角度来看,DCC方法可以被视为量子系统与经典环境相互作用的自洽波粒二象描述,对后续理论发展具有指导意义。
通讯作者:王林军,浙江大学化学系教授,主要研究方向为非绝热动力学理论与复杂功能材料机制模拟。
课题组主页:http://www.linjun-wang-group.com/
文 字:王林军教授课题组
编 辑:黄珍珍、张维娅
审 核:林旭锋
终 审:丁立仲

